Memahami Himpunan dalam Matematika Kelas 7 Kurikulum Merdeka

Memahami Himpunan dalam Matematika Kelas 7

 

Pendahuluan:

Matematika merupakan salah satu mata pelajaran yang membantu kita memahami berbagai konsep dan struktur dalam kehidupan sehari-hari. Salah satu topik yang diajarkan di kelas 7 adalah Himpunan. Himpunan merupakan kumpulan objek yang dapat didefinisikan dengan jelas. Dalam artikel ini, kita akan membahas konsep-konsep dasar himpunan berdasarkan instruksi seorang guru kepada siswanya.

 

Instruksi Guru dan Hasil Pengerjaan Siswa:

Guru memberikan dua instruksi kepada siswanya:

1. Buatlah kumpulan bilangan unik dari 1 sampai dengan 10.

2. Buatlah kumpulan bilangan prima dari 1 sampai dengan 10.

Instruksi pertama menghasilkan jawaban yang bervariasi di antara siswa karena interpretasi kata "unik" dapat berbeda-beda. Namun, pada instruksi kedua, semua siswa menghasilkan jawaban yang sama, yaitu {2, 3, 5, 7}, karena definisi bilangan prima yang jelas.

 

Definisi Himpunan:

Dari kasus di atas, kita dapat memahami bahwa himpunan adalah kumpulan objek yang dapat didefinisikan dengan jelas. Notasi himpunan dituliskan dengan huruf kapital seperti A, B, C, dst., dan anggota-anggota himpunan ditulis di antara kurung kurawal { }.

 

Contoh Pemahaman Himpunan:

Misalkan A adalah himpunan bilangan asli kurang dari 5. Ada tiga cara untuk menyatakan suatu himpunan:

1. Dengan pernyataan terbuka:  A = himpunan bilangan asli kurang dari 5

2. Dengan daftar anggota himpunan: A = {1, 2, 3, 4}.

3. Dengan notasi pembentuk himpunan: A = {x | x < 5, x = bilangan asli.

Diagram Venn digunakan untuk memvisualisasikan himpunan.

Himpunan Semesta dan Himpunan Kosong:

Guru memberikan instruksi membuat himpunan A adalah bilangan asli kurang dari 1 dan himpunan B adalah bilangan prima kurang dari 2. Siswa awalnya bingung karena instruksi tersebut menghasilkan himpunan kosong. Himpunan kosong (\(\emptyset\) atau \(\{\}\)) adalah himpunan yang tidak memiliki anggota. Sebaliknya, himpunan semesta adalah himpunan yang memuat semua objek atau anggota yang sedang dibicarakan.

 

Sifat-Sifat Himpunan:

1. Kardinalitas Himpunan: Menunjukkan jumlah anggota dalam suatu himpunan.

2. Himpunan Bagian: Hubungan antara himpunan bagian dan himpunan utuh.

3. Himpunan Kuasa: Kumpulan semua himpunan bagian dari suatu himpunan.

4. Kesamaan Dua Himpunan: Kapan dua himpunan dikatakan sama.

 

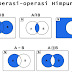
Operasi Himpunan:

Dalam artikel ini, kita juga membahas empat operasi himpunan utama, yaitu Irisan, Gabungan, Komplemen, Selisih, dan Perbedaan Simetris, beserta contoh-contohnya.

 

1. Irisan

Irisan adalah suatu himpunan yang elemennya merupakan elemen dari himpunan A dan B, Irisan himpunan A dan B disimbolkan dengan  A ∩ B, Contoh dari irisan himpunan adalah

A = {a,i,u,e,o} ; B = {a,b,c,d,e}

A ∩ B = {a,e}

2. Gabungan (Union)

Suatu himpunan yang elemennya merupakan gabungan elemen dari himpunan A dan B, Gabungan disimbolkan dengan  A ∪ B, Contoh dari Gabungan adalah

A = {7,9,11,13}; B = {b,c,d,f,g}

A ∪ B = {7,9,11,13,b,c,d,f,g}

3. Komplemen

Komplemen himpunan A adalah suatu himpunan yang anggotanya merupakan anggota S (himpunan semesta)  tetapi bukan anggota A, Komplemen disimbolkan dengan  A’, Contoh dari komplemen himpunan A adalah :

S = {2,3,5,7}; A = {1,3,5,7}

A’ = {2}

4. Selisih (Difference)

Selisih (difference) dari himpunan A dan B adalah himpunan yang anggotanya merupakan anggota A tetapi bukan anggota B, Selisih disimbolkan dengan A – B, Contoh :

A = {a,b,c,d} B = {a,i,u,e,o}

A – B = {b,c,d}

5. Perbedaan Simetris

Perbedaan simetris adalah himpunan A dan B  yang elemennya ada pada himpunan A atau B tetapi tidak pada keduanya, disimbolkan dengan A ⊕ B, Contoh :

A = {1,3,5,7,9}; B = {1,2,3,4,8}

A ⊕ B = {2,4,5,7,8,9}

Sifat-sifat Operasi Himpunan:

1. Sifat Idempoten: Irisan dan gabungan suatu himpunan dengan dirinya sendiri.

2. Sifat Identitas: Irisan dan gabungan suatu himpunan dengan himpunan kosong atau himpunan semesta.

3. Sifat Komutatif: Urutan himpunan dalam operasi tidak mempengaruhi hasil.

4. Sifat Asosiatif: Hasil operasi tidak bergantung pada cara mengelompokkan himpunan.

5. Sifat Distributif: Hubungan antara gabungan dan irisan dalam operasi.

EMBUN PAGI